On modeling advertising funnel with multi-task learning

While it is definitely not the greatest thing that appeared on the internet (if you value your user experience or privacy anyway), advertising on digital medium has proved to be a formidable source of revenue for many companies, and in particular the tech behemoths that today dominate this industry. And where there is money, there usually is innovation.

The advertising problem

The digital advertising problem is rather simple conceptually: it is about matching a demand from advertisers eager to pay good money and a supply of websites that would rather monetize their contents by displaying ads to wandering users. As you can imagine, the amount of ad opportunities generated from user visiting websites is usually very large, in comparison to the advertiser demand (arguably it could be considered infinite). In addition, while paying good money, advertisers also have the natural desire to generate some value from their investments, usually measured through business metrics such as click-trough-rate (CTR), bounce rate, or conversion rate (CVR).

Hence, ad systems can’t really be very successful by uniformly printing random ads on random ads opportunities but need a smarter process to decide if an ad opportunity is worth it, given a finite set of ads from advertisers. This smarter process usually involves a ranking system: given some context encoding the ad opportunity, it ranks all available ads from a finite set, with respect to some metric, and either push the first one, or sample one non uniformly using the metric used to rank.

The advertising funnel

Now there is a distinction to make in the goals advertisers usually have: they either want to be known and assert their online presence, or they want to generate user engagement and capture traffic to their own websites to generate organic revenue. The first kind of objective usually isn’t too demanding - in terms of the ad system complexity that is - as advertisers will be satisfied as long as somebody actually sees the ad slot it bought. The second objective is the one that interest us here and is more complex to efficiently pull off.

User engagement is not a binary quantity describing “interested” and “not interested” similar to a “seen”, “not seen” that the first objective would be about. Instead, it is a number of steps with a causal structure to it encoding a degree of interest of an user. In the advertising lingo, it’s called a funnel, and in practice it is specific to what advertisers want.

In simple term, a funnel describes different steps in the user engagement process, and the deeper it goes, the more interested in the service/product/whatever the user is assumed to be. Let’s take an example:

stateDiagram-v2
    direction LR

    state click_fork <<fork>>
    [*] --> click_fork
    click_fork --> Click
    click_fork --> Scroll
    Click --> [*]

    state visit_fork <<fork>>
    Click --> visit_fork
    visit_fork --> Visit
    visit_fork --> Bounce
    Visit --> [*]

    state conversion_fork <<fork>>
    Visit --> conversion_fork
    conversion_fork --> Conversion
    conversion_fork --> Leave
    Conversion --> [*]

Note that each step in the funnel is a binary event: either there is some degree of engagement (such as a click), unlocking the possibility to reach the next step in the funnel, or there is not and it ends there. Moreover, the deeper the action in the funnel, the more valuable it is assumed to be, simply because the more correlated it is to the revenue of the advertiser.

The classic approach

Recall the ranking system mentioned a few lines above. A very useful information to build an efficient score is an estimate of the probability of occurrence of funnel events, such as clicks, visits and conversions, given an ad opportunity context. The probability of a funnel event is proportional to the potential revenue an advertiser can generate, and it turns, the revenue an ad system can generate.

As funnel events are binary in nature, they can be modeled by Bernoulli trials with probability $p_{event}$ and because ad opportunities can be considered i.i.d, funnel events realizations $y_{event}$ are assumed independent. This makes them good problems to be solved with machine learning methods as they are basically threshold-free binary classification tasks (threshold-free because we’re not interesting in predicting a class but rather a probability of observing the positive class).

A simple way of doing so for every funnel events is to build individual prediction models: one CTR model, one model predicting a visit rate and another one dedicated to conversions predictions. Our example funnel is then described by the triplet of independent models

\[(\mathcal{M}_{click}, \mathcal{M}_{visits}, \mathcal{M}_{conversions})\]

such that

\[\mathcal{M}_i : \mathcal{X}_i \mapsto \mathcal{Y}_i\]

is a learned mapping between i.i.d context vectors in $\mathcal{X}_i$ and funnel events observed feedbacks, effectively describing the probability distribution of our events. Linear models such as logistic regressions or deep learning models outputting a probability have been widely used for that because they can also provide some theoretical guarantees that predicted probabilities are rather well calibrated.

Towards a multi-task learning paradigm

While it provides flexibility to a certain extent, a system of independent models has some drawbacks:

• it requires as many training and inference pipelines as there are events in the funnel to be predicted, increasing the system complexity and mechanically reducing its robustness and maintainability.
• Every models being independent, it’s not possible to encode some special properties of the problem. In particular, it’s difficult to enforce that $ P(click \mid \textbf{x}) \geq P(visit \mid \textbf{x}) \geq P(conversion \mid \textbf{x}) $ for some input context $\textbf{x}$.
• For the same reason, there is no way to allow the different prediction tasks to share information, which could improve predictive accuracy on some tasks by taking advantage of other correlated tasks that could be simpler.

In a multi-task setting, we can instead build a single model that directly learns the joint probability distribution $ p(click, visit, conversion \mid \textbf{x}) $ of our tasks, given a context vector $\textbf{x}$ for every opportunity, and a vector of labels $\textbf{y}$ containing observed feedbacks for a click, visit, conversion or any other event.

Problem formulation

Now each task has its own loss function $\mathcal{L}_t$ and a global, multi-objective loss function to be minimized is defined by:

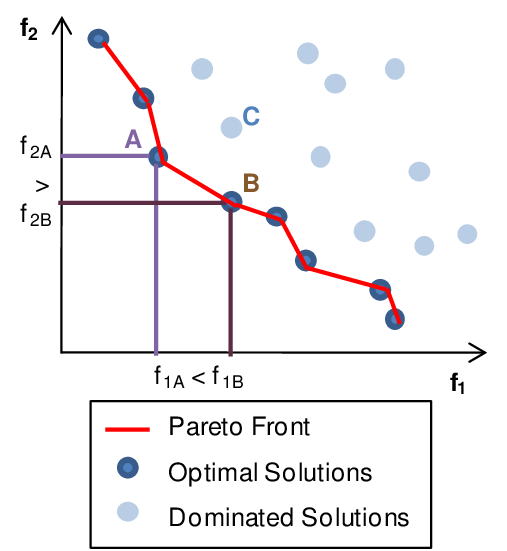
\[\text{arg min}_{\theta} = g( \mathcal{L}_{1}, ..., \mathcal{L}_{t}; \theta )\]

This problem corresponds to finding a Pareto optimum of the model parameters that minimizes the value of this multi-variable function. In this context, Pareto optimality refers to a solution such that it is not possible to further improve an individual loss without degrading another one (for instance in our example, improve the CTR model would decrease the CVR model).

As our optimization procedure of model training still need a scalar loss function to minimize, a simple approach is to scalarize the multi-objective by defining $g$ as a real valued function $g: \mathbb{R}^T \mapsto \mathbb{R}$. The simplest of such functions is a linear combination of the individual task losses:

\[g( \mathcal{L}_{1}, ..., \mathcal{L}_{t} ) = \sum_{t} w_{t} \mathcal{L}_{t}\]

and is called linear scalarization of a multi-objective loss function. Note that is introduces the additional hyper-parameters $w_t$ controlling the influence of the various tasks in the optimization procedure.

For example, let’s take our simple funnel example from before with 3 events: clicks, visits and conversions. Then the scalarized multi-objective function could be defined as:

\[\mathcal{L} = w_{click} \mathcal{L}_{click} + w_{visit} \mathcal{L}_{visit} + w_{conversion} \mathcal{L}_{conversion}\]

Going further, we might also need to take into account the fact that our tasks exists in different sample spaces. Indeed, one property of the funnel we saw is that a visit necessarily comes after a click, hence the set of visits is smaller or equal than the set of clicks. A simple way to encode this information is to add indicators functions in each task losses in order to only make a given sample contributes to the loss if it is in the task sample space. In our example, we would define losses for visit prediction and CVR tasks as:

\[\mathcal{L}_{visit} = \frac{1}{\mid \mathcal{C} \mid} \sum_i \textbf{1}_{[y_{click}^{i} = 1]} \mathcal{L}_{visit}^{i}\] \[\mathcal{L}_{conversion} = \frac{1}{\mid \mathcal{V} \mid} \sum_i \textbf{1}_{[y_{visit}^{i} = 1]} \mathcal{L}_{conversion}^{i}\]

The flexibility of combining multiple loss corresponding to multiple objectives optimized jointly also allows to encode the causal nature of the funnel - that is, $P(click) \geq P(visit) \geq P(conversion)$. Indeed, we can easily transform this hard constraint into a soft penalty in the loss function in a similar fashion to what is usually done with weight decay avoiding overfitting in a deep learning model. This penalty term increases the loss if the previous constraint is violated, and contributes nothing otherwise. Ideally, it would make the model converge to a solution satisfying this additional constraint (at the cost of perhaps a harder convergence).

\[\mathcal{L}_{causal} = \frac{1}{N} \sum_i [ \max( \hat{y}_{visit}^i - \hat{y}_{click}^i, 0) + \max( \hat{y}_{conversion}^i - \hat{y}\_{visit}^i, 0) ]\]

Challenges of multi-task learning

Even if it can provide a great simplification of training and inference pipelines by combining multiple predictions tasks in one model, multi-task learning also has its challenges. In particular there is often a degradation in the predictions quality compared to single independent models when tasks have different learning dynamics:

• non-aligned gradients that make the global loss function slow to converge as well as make it difficult to find a Pareto optimum. In this case the performance on the different tasks can be lower compared to the independent model approach.
• Different loss landscapes can make the norms of the gradients very different across tasks, biasing the learning procedure toward a few tasks.
• If the number of training samples is widely different across tasks, the learning procedure can be biased toward the over-represented task.
• Kinda intuitive, but if tasks are inherently too different or heterogenous, all Pareto optimums might simply lead to worse performance on individual tasks compared to the independent model approach.
• There is some subjectivity in how the tasks should be prioritized during the learning procedure. Indeed perhaps there is some tradeoff on Pareto optimums depending on the product. For instance if clicks generate more revenue, it might not be a good idea to prioritize conversions during training if its degrade click prediction.

Model architectures

While it seems to exist a whole taxonomy of architectures for multi-task learning, relevance of those definitely depends on the tasks they try to solve, and in particular the modality of the input data. This post being about ad funnel, we probably deal with tabular data encoding an ad opportunity. In that case, about three kind of architectures seem to be widely used to solve the problem described above:

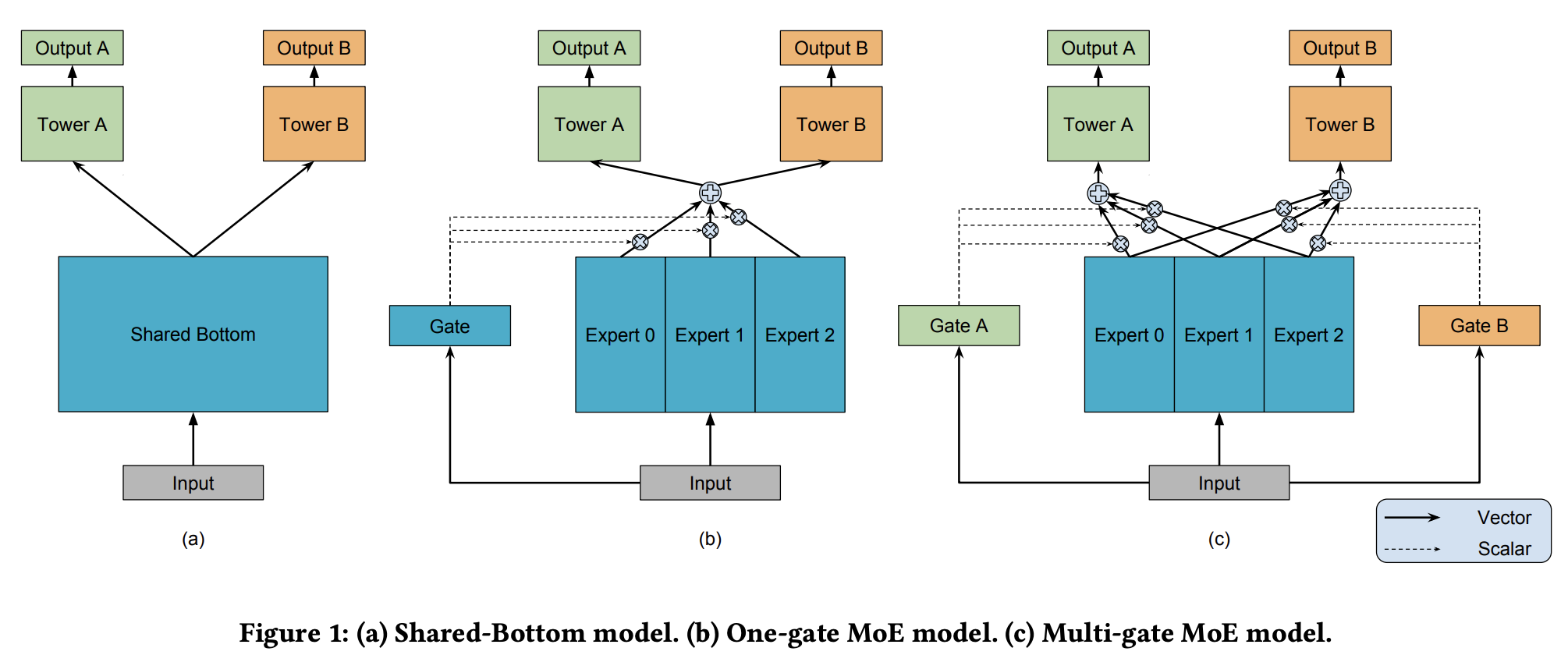
1. Shared bottom, where the input is projected into a latent space common for all the tasks. The latent representation is then used as inputs for task-specific encoders - so called “Towers” in the literature - projecting again is task-specific latent spaces, and there are as many towers as tasks. The shared encoder allows to learn a shared representation of the input data.

2. Mixture of Experts (not to be mixed with the LLM architecture pattern) where instead of a single shared one, there are many encoders, so called “experts”, that project the input in distinct latent spaces to provide different views. On top of this set of expert encoders, there is a gating network whose role is to build a combination of exerts representations conditioned on the input. Then just like the previous architecture, this mixed representation is used as input by each task-specific encoders that further process it to adapt it to their respective task.

3. Multi-gate Mixture of Experts, which is a slight modification of the previous MoE architecture. Here there also is a set of shared encoders that build different views of the same input, but instead of one global gating mechanism, there are as many as there are tasks. The rationale behind this is to provide each tasks with their own process to combine experts latent representations, allowing a gating network to focus on what is relevant for its tasks. Again the last layers don’t change.

Note that encoders can be anything: from the simplest MLP to a Transformer. Usually, gating networks are MLP with softmax on the output, taking the context vector as input and outputting a vector of the same size of the number of experts:

\[\text{Gating} := Z_e \cdot \text{softmax}(\text{MLP}(\textbf{x}))\]

where $Z_e = [\textbf{z}_i]$ a matrix of dimension (dim_hidden_expert, num_expert) and $\text{softmax}(\text{MLP}(\textbf{x}))$ is a vector if dimension (num_experts,) such that the result is a linear combination of the experts representations, weighted by the gate scores.

Note that an additional temperature parameter can be introduced in the softmax to control the severity of the gating selection process.

\[\text{softmax}(\textbf{x}; T)_i = \frac{e^{ \frac{x_i}{T}}}{ \sum_j e^{ \frac{x_j}{T}} }\]

Indeed, the softmax converges to a uniform distribution as the temperature goes to $+\infty$ and to an argmax as the temperature goes towards 0. A high temperature would tend to make each experts weight equally (also inhibiting the gating network as it would in effect result in a simple mean over experts) while a low temperature would force the experts to specialize in only one task as the gating network would only route one expert representation to one task.

Implementation

I implemented (in TF, sorry) the three simple architecture described above here. They are not really optimized and use MLP for encoders as an example. Nevertheless it’s flexible enough to be adapted without too much trouble, the harder thing being scaling rather than modeling.